Breaking Permutation Security in LLM Inference
Arka Pal , Erica Choi , Rahul Thomas , Louai Zahran , Micah Goldblum 6 months ago
Further details on this blog post can be found in our arXiv paper and associated code repository
In the previous blog post, we explored the recent history of SMPC (Secure Multi-Party Computation) approaches to performing privacy-preserving inference of LLMs - that is, requesting an untrusted third party to do the inference for you, while ensuring that they cannot see your prompt/data.
We saw that despite significant recent progress, SMPC approaches remain prohibitively slow to use for modern LLMs. Therefore, recent works have instead proposed to replace cryptographic security throughout the protocols with statistical security instead. Specifically, as the non-linearities within the LLMs are often the most computationally expensive portion of SMPC protocols, recent works propose to compute them on permuted plaintext - exploiting the fact that the nonlinearities can work ‘as-is’ on permutations (a property called permutation-equivariance).
The security of this approach - whether the untrusted third party can read your prompt - is dependent primarily on how hard it is to reverse-engineer the permuted plaintexts into the original prompt. At first glance, this might seem very difficult; after all, the ‘plaintext’ in consideration here - LLM ‘hidden states’ - have the size of thousands of dimensions for modern models. For any vector of size N, there are N! ways to permute it. Thus for a hidden state size of 1000, the number of possible permutations is 102567. The number of atoms in the universe is around 1082, so even if every atom became its own parallel processor to check the possibilities, and you operated a check every 10−43 seconds (every Planck time), it would still take an inconceivable amount of time to check all the possibilities - many times longer than the age of the universe. Furthermore, the space of permutations is a discrete one. In many settings, optimizing over a large set of discrete options is much harder than doing so over a continuous set.
However, it turns out in practice, and especially for open-weights LLMs, permutations are insecure. Below, we demonstrate a novel attack that has ~100% accuracy in decoding and takes only a few minutes to execute.
Setting
We consider the general case where there are k parties Pk participating in inference, and a particular party has access to a permutation of the hidden states h=[h1,h2,…,hN] - where N is the number of tokens in the prompt - at some layer L of the LLM. This is a typical setting for permutation-based MPC protocols, such as PermLLM, STIP, and Centaur, which we described in more detail in our previous blog post. We consider the open-weights setting, where the LLM weights are known to all parties (extensions of our attack to the closed-weights settings of STIP and Centaur can be found in our paper).
Introduction and Warmup
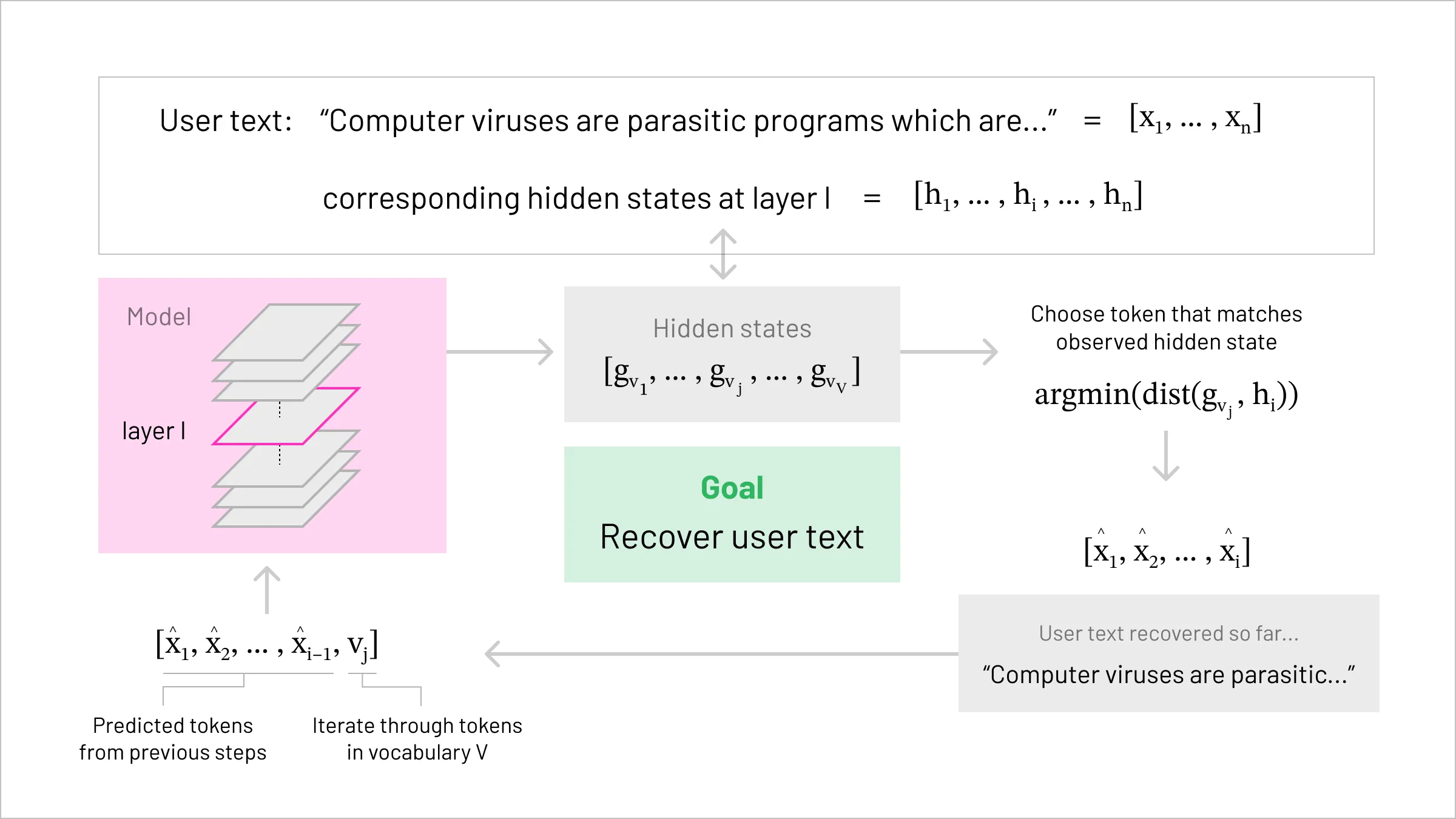
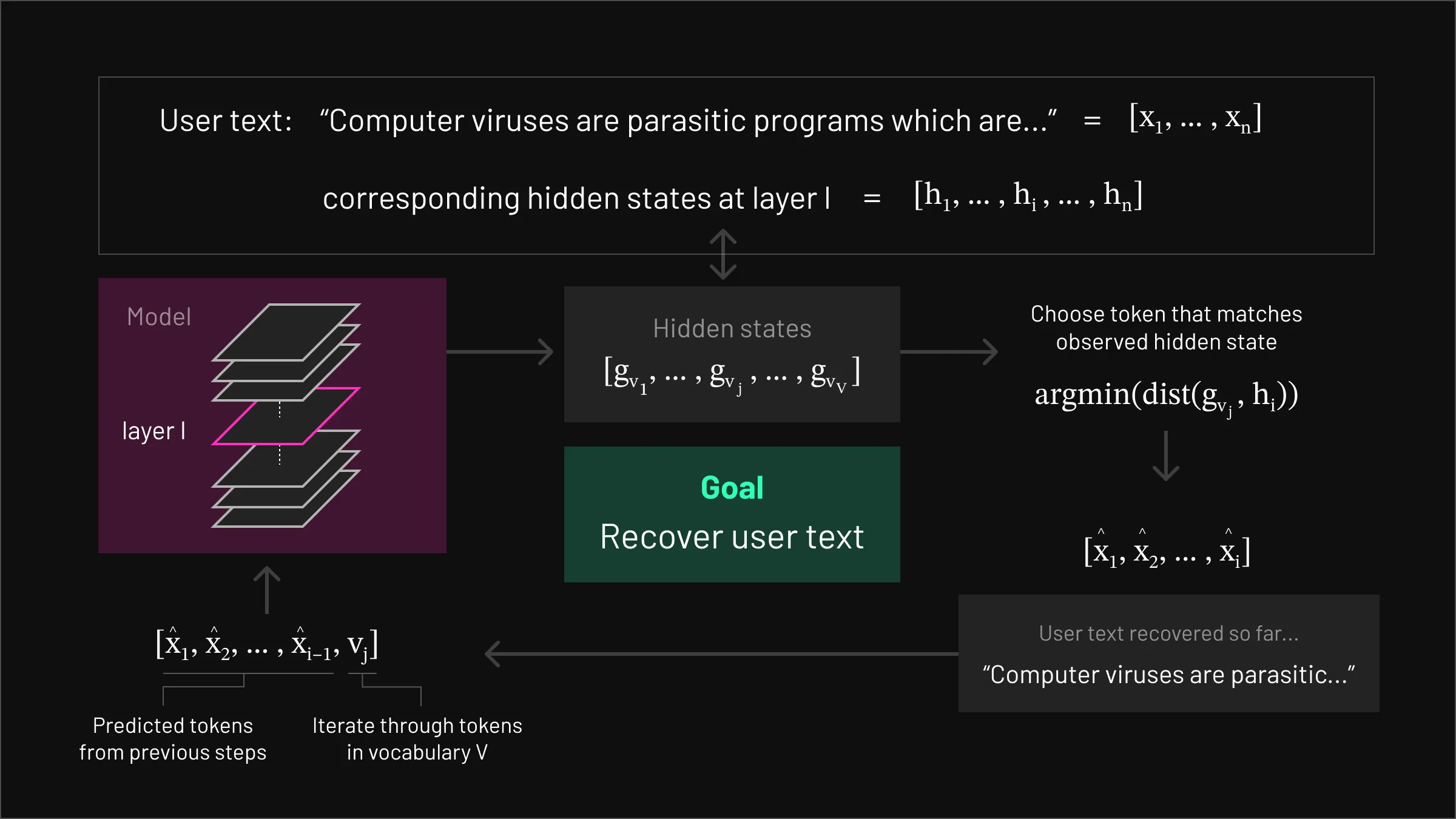 High-level representation of the vocab matching attack
High-level representation of the vocab matching attack The primary properties of LLMs that we will exploit for our new attack are:
- The vast majority of recent LLMs - such as GPT, Llama, DeepSeek, etc - are decoder-only LLMs. This means that each token that is generated depends only on the tokens before it.
- LLMs take inputs, and produce outputs, over a fixed set of inputs - called their vocabulary. This is a list of tokens that constitute something akin to a unique alphabet for each LLM (here is an introduction to tokenizers).
Warmup
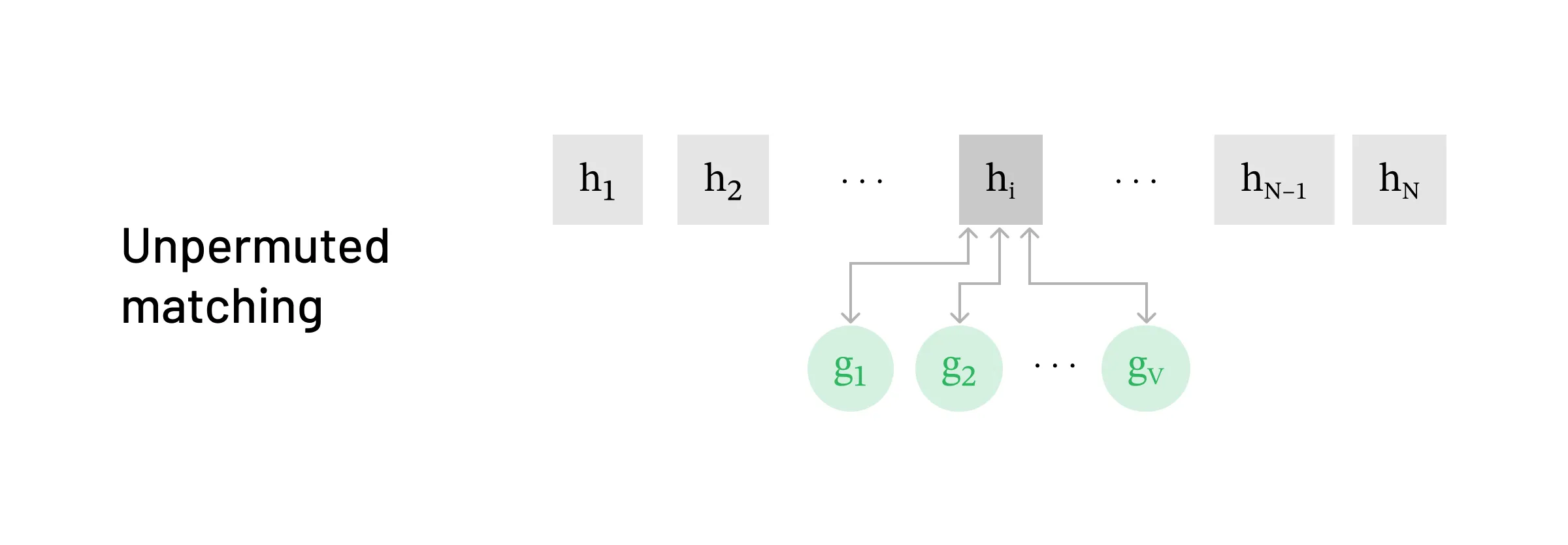
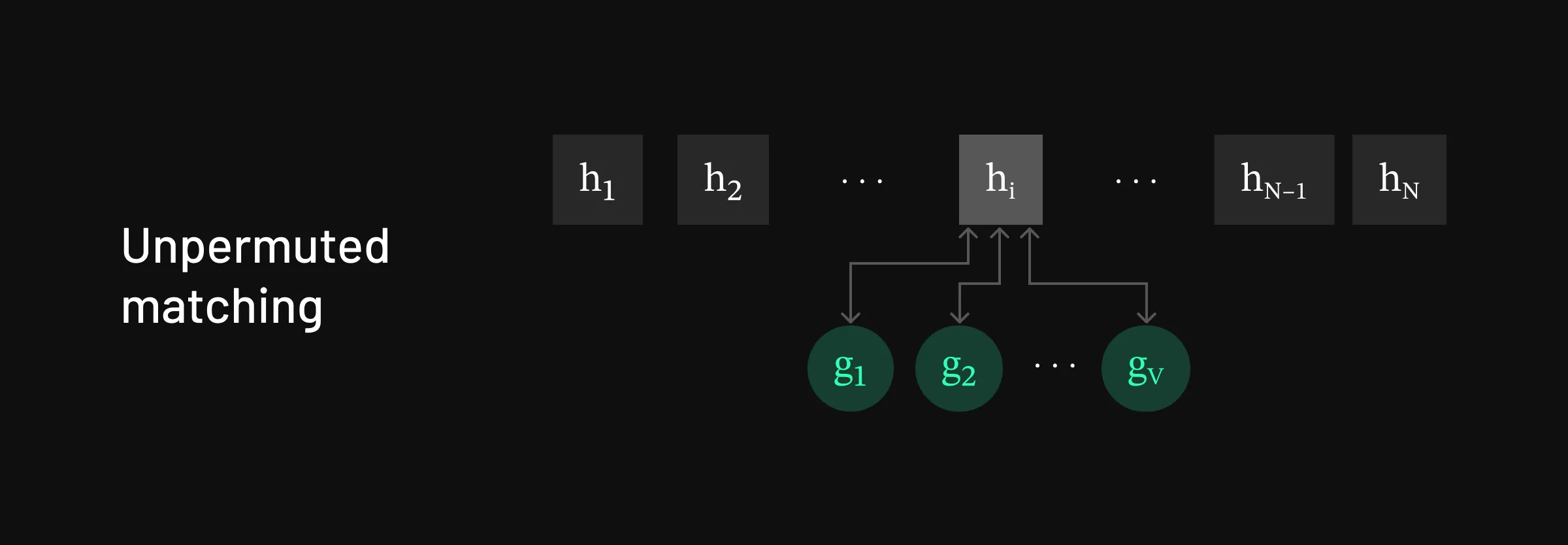 Strategy for matching in the unpermuted setting
Strategy for matching in the unpermuted setting As a warmup and introduction to our attack, we’ll start by showing how to reverse unpermuted h=[h1,h2,…,hN] into the original tokens x=[x1,x2,…,xN].
The size of the overall search space for x is VN, where V is the size of the model’s vocabulary. This is infeasible for large V and/or large N, which is the case for most usage – V for many modern LLMs larger than 100,000, and prompts are typically anywhere from 20 to over 4000 tokens in length.
However, we can exploit the autoregressive property of LLMs to reduce the search space from exponential to linear. The basic attack proceeds as follows:
- First, we iterate through the tokens in the vocabulary, passing them through the LLM model, until we find a hidden state that matches the observed h1. As the first h1 only depends on this one token, we only need to search through a single token sequence here. At most, this will take V many tries.
- Having found the first token, we fix this, and now do forward passes over [x1,v] for all tokens v in the vocabulary, until we find a match to h2. Since h2 only depends on x1 and x2, and we already know x1 from the first step above, we again only need at most V many searches here.
- Repeat this procedure until all of [h1,…,hN] are matched.
That’s really it! The procedure is simple, and has worst-case complexity O(VN) - making this entirely feasible for a determined adversary to perform.
Practical Difficulties
Even though the above idea is conceptually simple, making it work in practice runs into a key difficulty: we cannot assume that there will be a single, exact match for the observed hidden state at each step.
Two main issues contribute to this difficulty. The first is that the forward pass performed over the vocabulary is non-deterministic, meaning the same token doesn’t always produce exactly the same hidden state. Several factors such as the order of computations, differences in hardware, random number seeds, environment variables, and the state of initialized memory on the machine can all introduce small but significant differences in the output.
A natural workaround is to relax the matching requirement from ‘exactly the same’ to ‘close enough,’ but this brings us to the second challenge: collisions. If too many different tokens produce hidden states that are similar to the target, we can end up with multiple possible matches at each step. This causes the search space to grow exponentially. If the number of matches at each step is M, we have to search MN possible combinations of tokens in order to guess the correct sequence. Even modest values of M and N make this infeasible.
To overcome these issues, we adopt a two-step fuzzy matching strategy. First, we measure the distance between each candidate hidden state and the observed hidden state. Then, we accept a token as a match if this distance falls below a carefully chosen threshold. This approach allows us to account for small variations while still filtering out unlikely candidates, keeping the search space manageable. It is important to set the threshold correctly; if it is too high, then we will have too many matches (collisions), and if it is too low then we may not have any matches at all (due to the nondeterminism). Thus we calibrate the threshold on a small training set.
Efficiency
To speed up the attack further, rather than checking every possible token in an arbitrary order, we use a proposal model that ranks how likely each token is to appear next. This lets us prioritize the most probable candidates first. With this approach, we reduce the average number of tokens checked per step from half the vocabulary to typically around 100, giving us a more than 1000× speedup.
We also develop a custom version of key-value caching to cut down on the number of expensive computations needed during decoding. In transformer models, KV caching stores intermediate results called “keys” and “values” from previous steps, so the model doesn’t have to recompute them every time (here is an introduction to KV caching). By extending and adapting this idea to our attack setting, we further reduce overhead and latency.
Together, these improvements bring the decoding time for prompts of length 50 down from many hours to typically less than 2 minutes.
Experimental Results
Surprisingly, we find that it is quite easy to set threshold values that ensure good matches and no collisions at all. Our experiments, conducted on Gemma-2-2B-IT and Llama-3.1-8B-Instruct, search for the optimal threshold value by examining results on prompts of length 50. Applying this threshold value to 1000 held out prompts confirm the effectiveness of this method; we are able to decode nearly 100% of the prompts perfectly:
 The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the unpermuted setting.
The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the unpermuted setting. Decoding Permutations
In the warmup above, we were able to reverse unpermuted hidden states of LLMs nearly perfectly. It turns out that extensions to the above attack enable reversal of permuted hidden states as well - even though the complexity of the problem appears to have grown astronomically.
Recall that for h=[h1,h2,…,hN], N is the number of tokens in the prompt (the “sequence dimension”) and each hi is a d-dimensional vector (here d is the “hidden dimension”).
Sequence Dimension Permutation
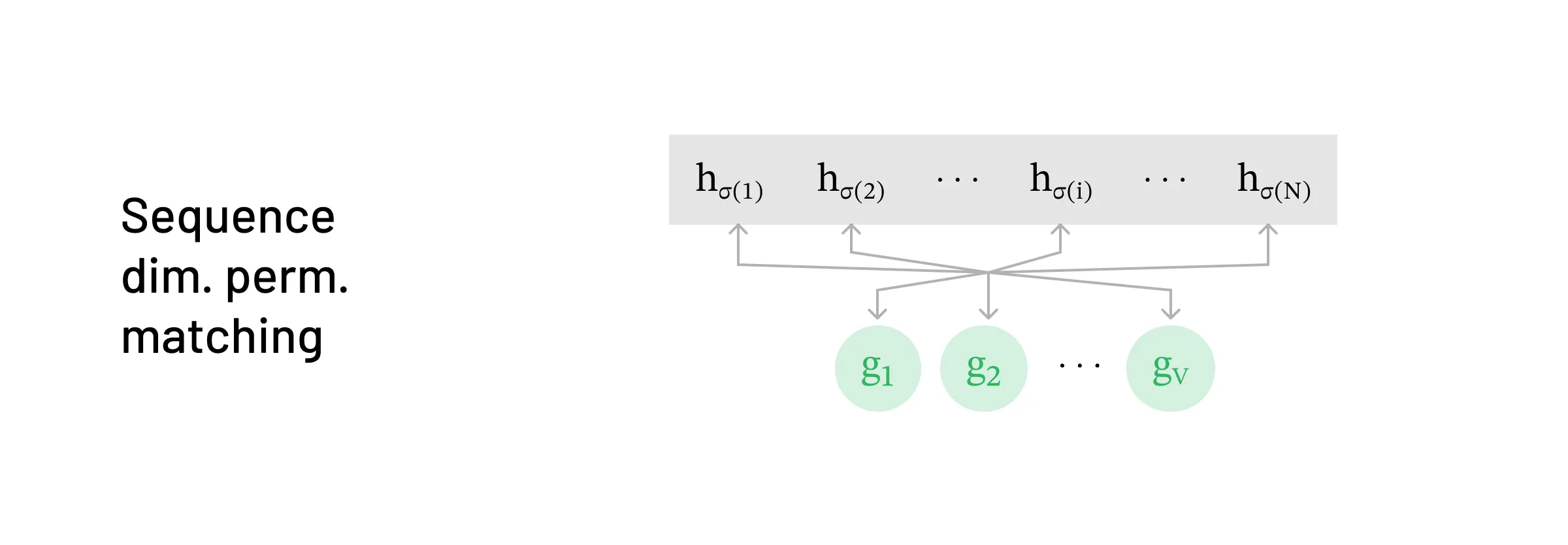
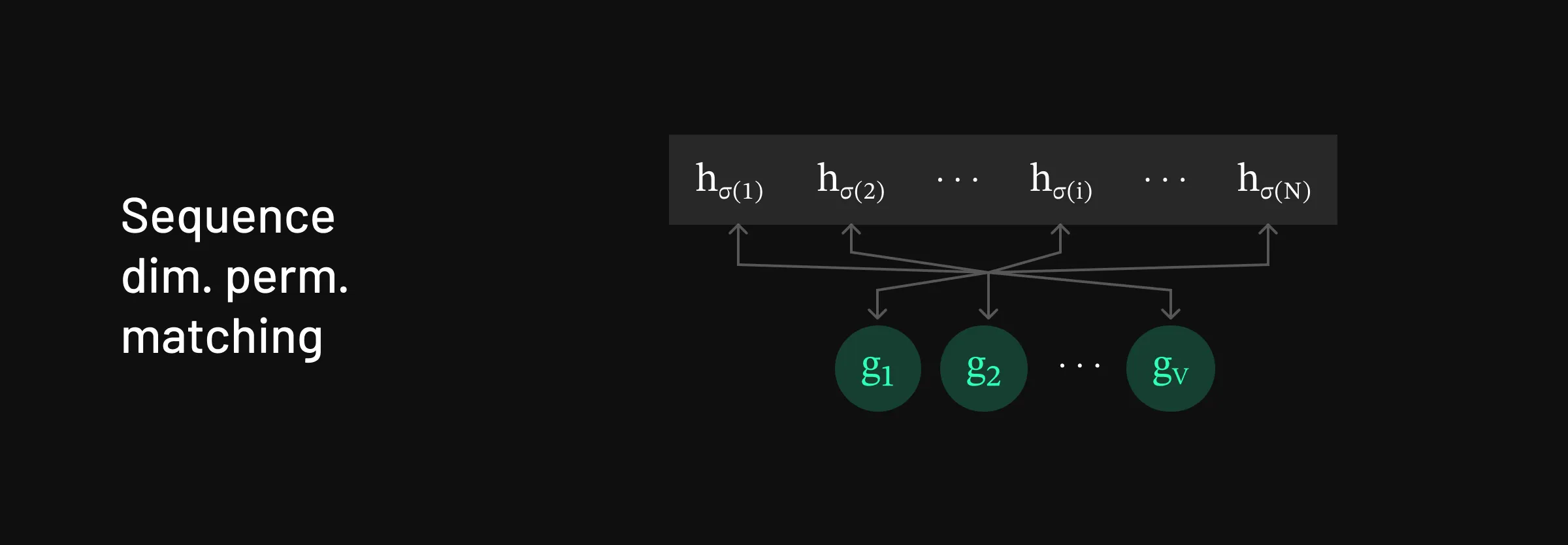 Strategy for matching in the sequence-dimension-permuted setting
Strategy for matching in the sequence-dimension-permuted setting First we look at permutation on the sequence dimension of h=[h1,h2,…,hN]. Mathematically we can write this permutation as:
hseq_perm=[hσ(1),hσ(2),…,hσ(N)]
where σ is a permutation of [N]=1,2,…,N.
For example: h=[h1,h2,…,hN] can be permuted to hseq_perm=[h2,h4,…,h1]
The modified attack proceeds as follows:
Similar to the basic attack, we iterate through the tokens in the vocabulary, passing them through the LLM model. However, since the target state is now permuted, instead of searching for a hidden state that matches h1, we need to find a hidden state that matches hσ(1)
- Here’s where the modification comes in. Since we don’t know what σ(1) is, we compare each hidden state produced by the candidate tokens to every hidden state in h. We select the token that matches some hidden state hi, hoping that i=σ(1).
- In fact, we know this will happen for exactly one hi, because exactly one of them is the first token in the sequence; all the others will not match anything in our vocabulary because they are later in the sequence, and so will have been modified by attention.
Now that we’ve found a match for hσ(1), we discard hσ(1) and fix the first token. Then we do forward passes over [x1,v] for all tokens v in the vocabulary until we find a hidden state that matches some hi. Note that here we only need to check for N−1 hi’s since we discarded hσ(1).
- Once again, by the properties of attention, we know there will be exactly one match at the second token position.
Repeat this procedure until all of [h1,…,hN] are matched.
The key insight is that even though the sequence of hidden states is permuted, there is exactly one ‘first token’, exactly one ‘second token’, and so on.
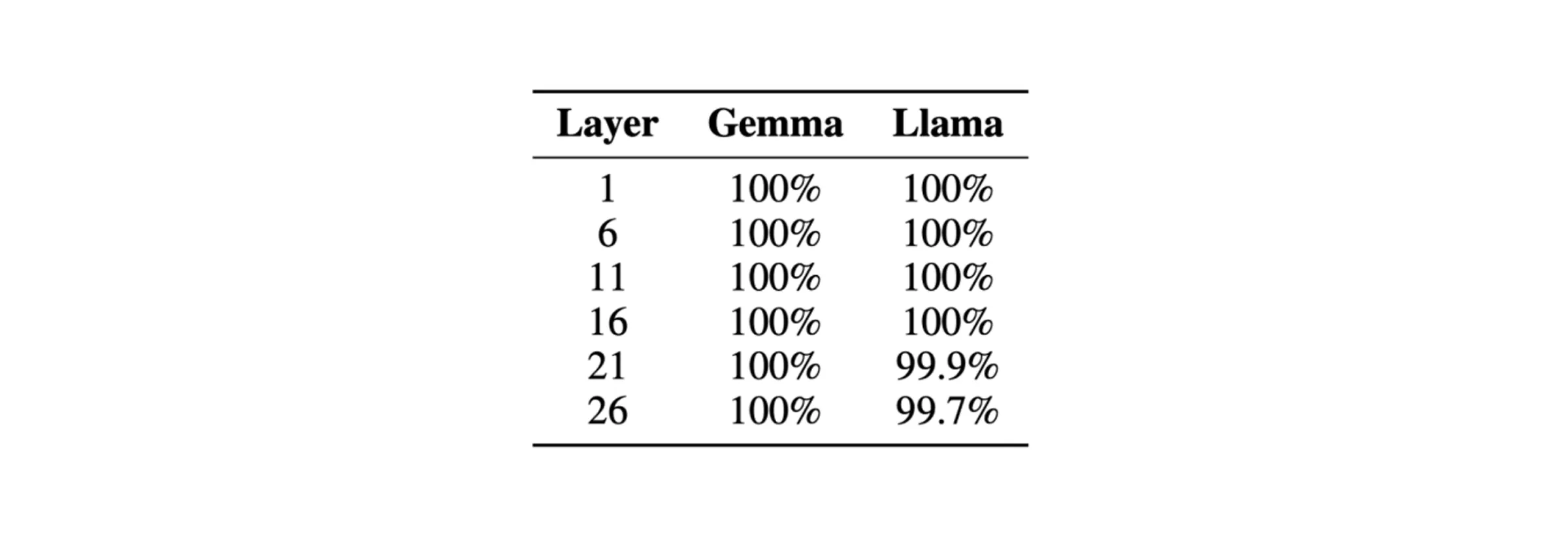
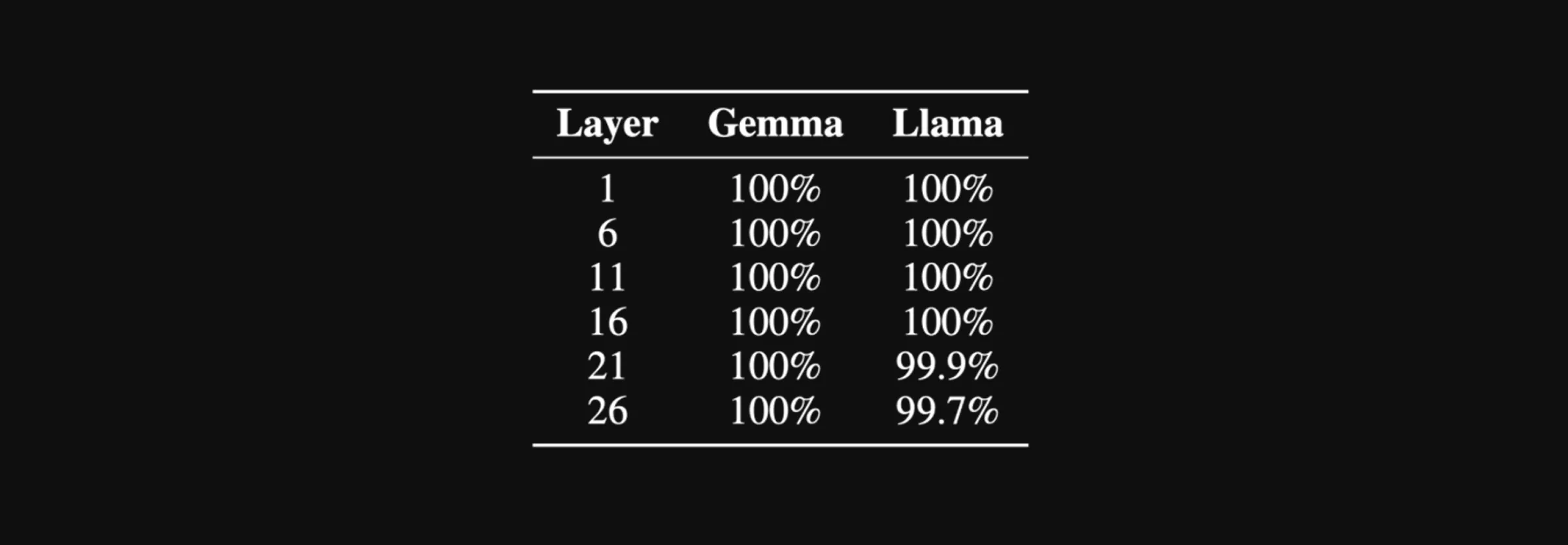
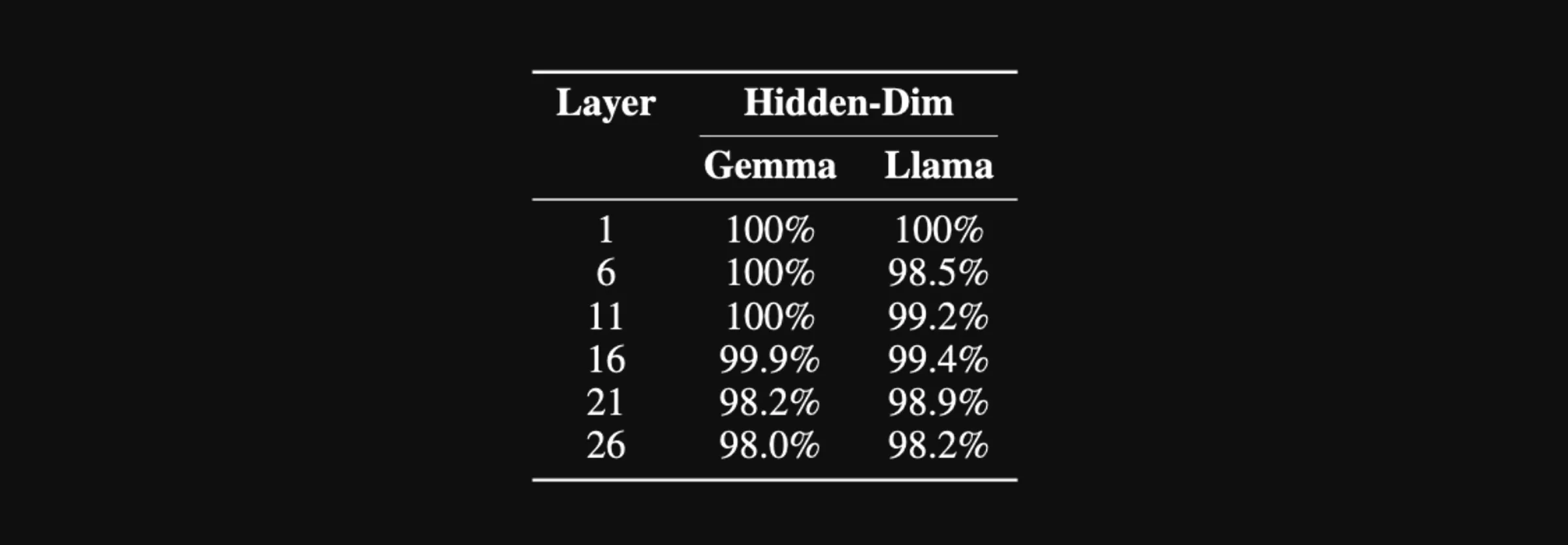
To test this modified scheme, we experimented with 1000 sample prompts using Gemma-2-2B-IT and Llama-3.1-8B-Instruct. For every fifth layer of the model, so layers 1, 6, 11, 16, 21, and 26, we took the hidden state of the prompt, applied the sequence dimension permutation, and used the described attack to recover the original, unpermuted prompt. Again, our results below show a near-perfect decoding for all samples:
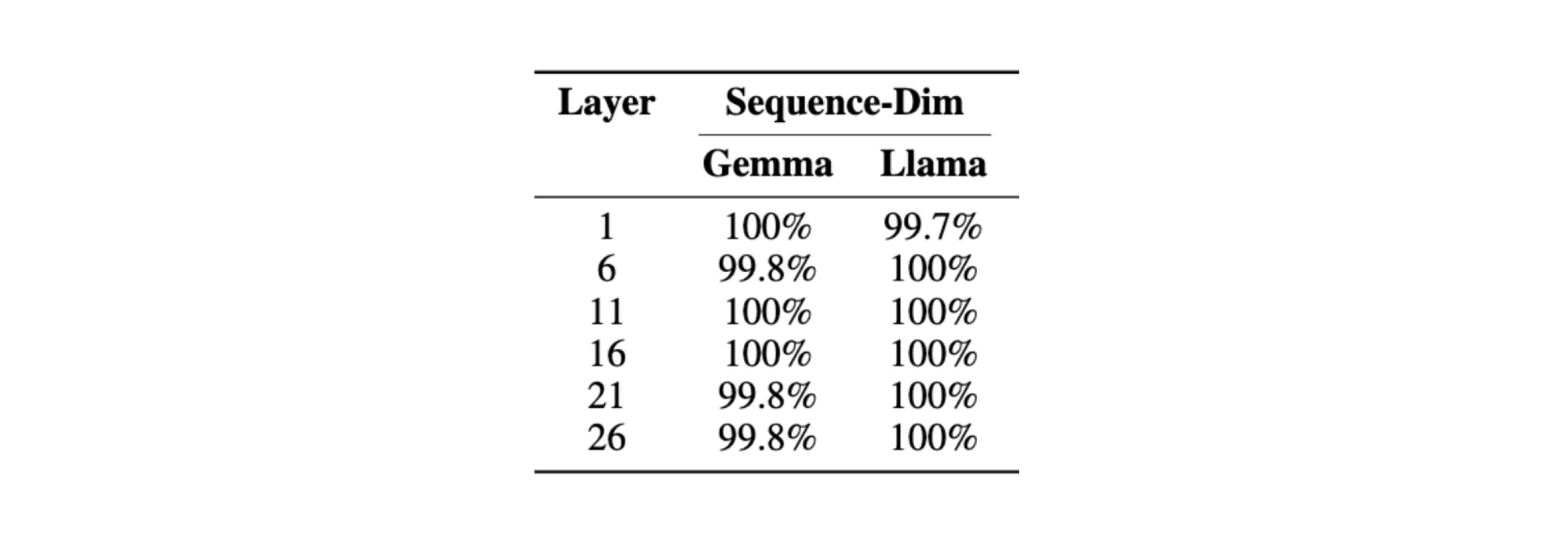
 The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the sequence-dimension-permuted setting.
The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the sequence-dimension-permuted setting. Hidden Dimension Permutation
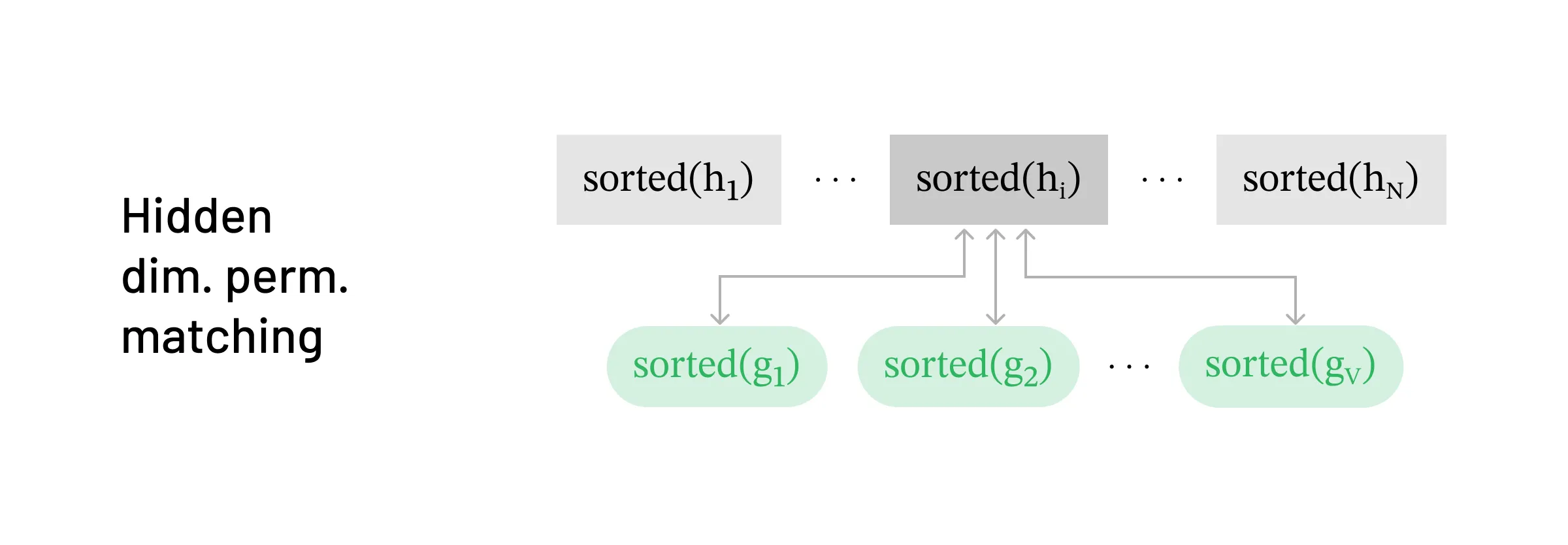
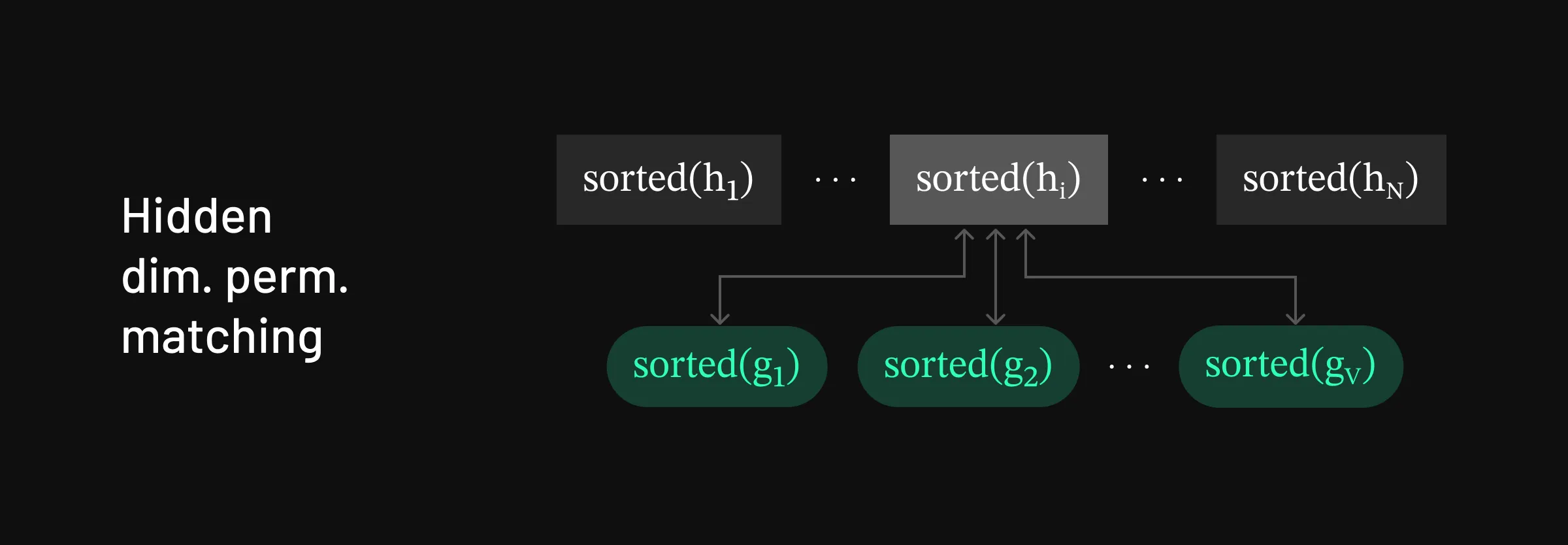 Strategy for matching in the hidden-dimension-permuted setting
Strategy for matching in the hidden-dimension-permuted setting Next, we show how to decode permutations on the hidden dimension of h=[h1,h2,…,hN]. Mathematically we can write this permutation as:
hhidden_perm=[π1(h1),π2(h2),...,πN(hN)]
where each πi permutes elements of a d-dimensional vector.
The modified attack proceeds as follows:
- We iterate through the tokens in the vocabulary, passing them through the LLM model. We want to find a match for π1(h1). Since it’s no longer possible to compare the vectors directly, we sort each vector to be compared. Here’s a simplified example. Say token x1 outputs hidden state g=[0.3,−0.5,0.6,0.1]. The permuted hidden state the adversary has could look something like π1(h1)=[0.6,−0.5,0.1,0.3]. To know that these are a match, we sort both g and π1(h1) to see that sorted(g)=[−0.5,0.1,0.3,0.6] is a match for sorted(π1(h1))=[−0.5,0.1,0.3,0.6].
- Having found the first token, we fix this, and now do forward passes over [x1,v] for all tokens v in the vocabulary, until we find a match to π2(h2).
- Repeat this procedure until all of [h1,…,hN] are matched.
The key property that hidden dimension permutation requires to be successful is that sorted hidden states are unique - i.e. there are rarely two hidden states that, when sorted, give the same vector. It turns out that this property also holds in practice.
Similar to the sequence dimension permutation experiments, we applied the hidden dimension permutation across layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct and used our sorting strategy to recover the original prompt. Again, our results show extremely effective decoding in this setting:
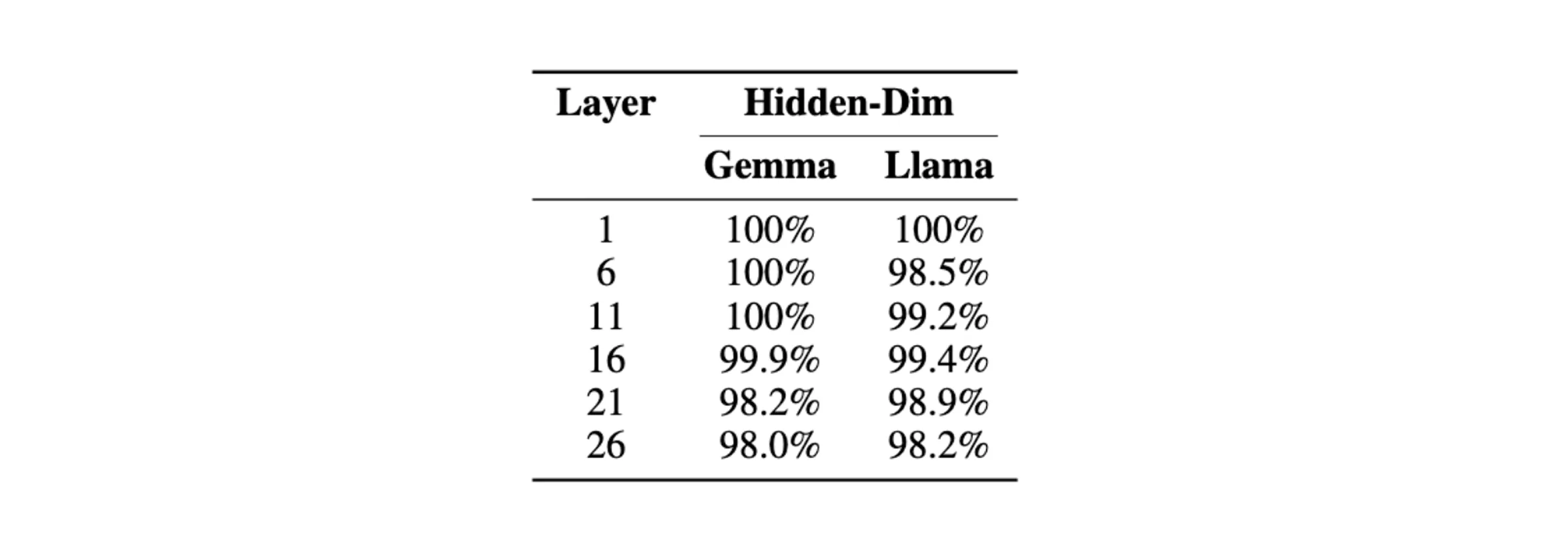
 The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the hidden-dimension-permuted setting.
The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the hidden-dimension-permuted setting. (Factorized) 2D Permutation
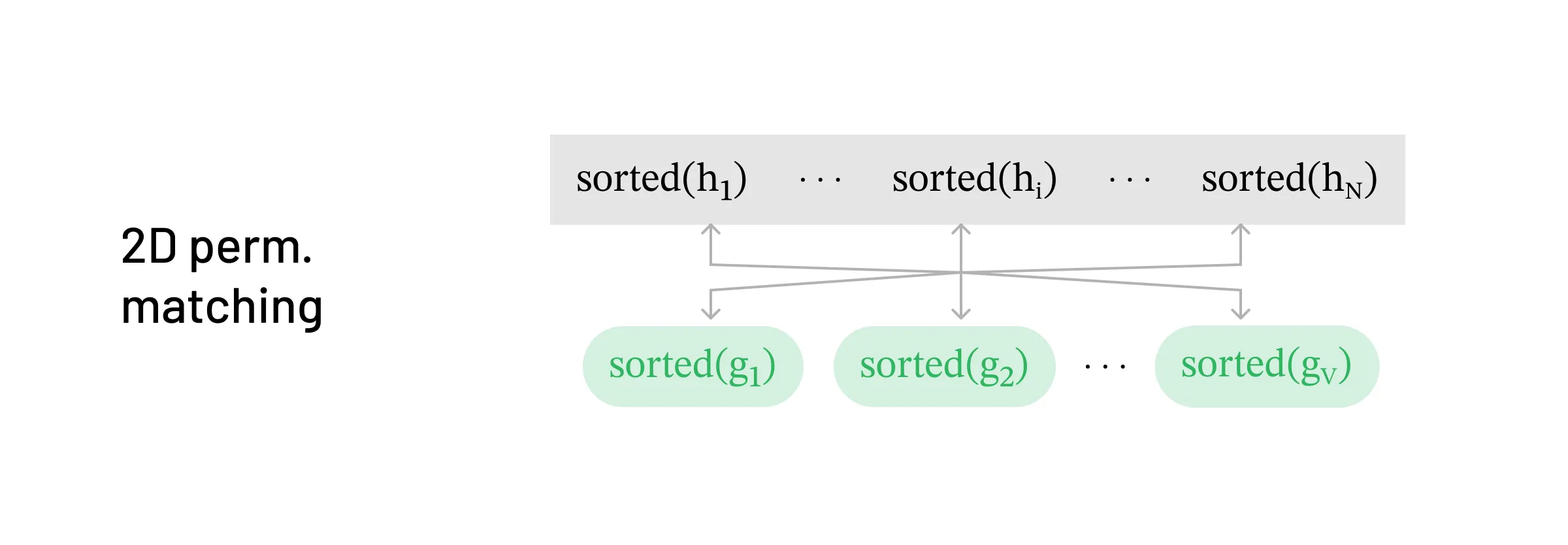
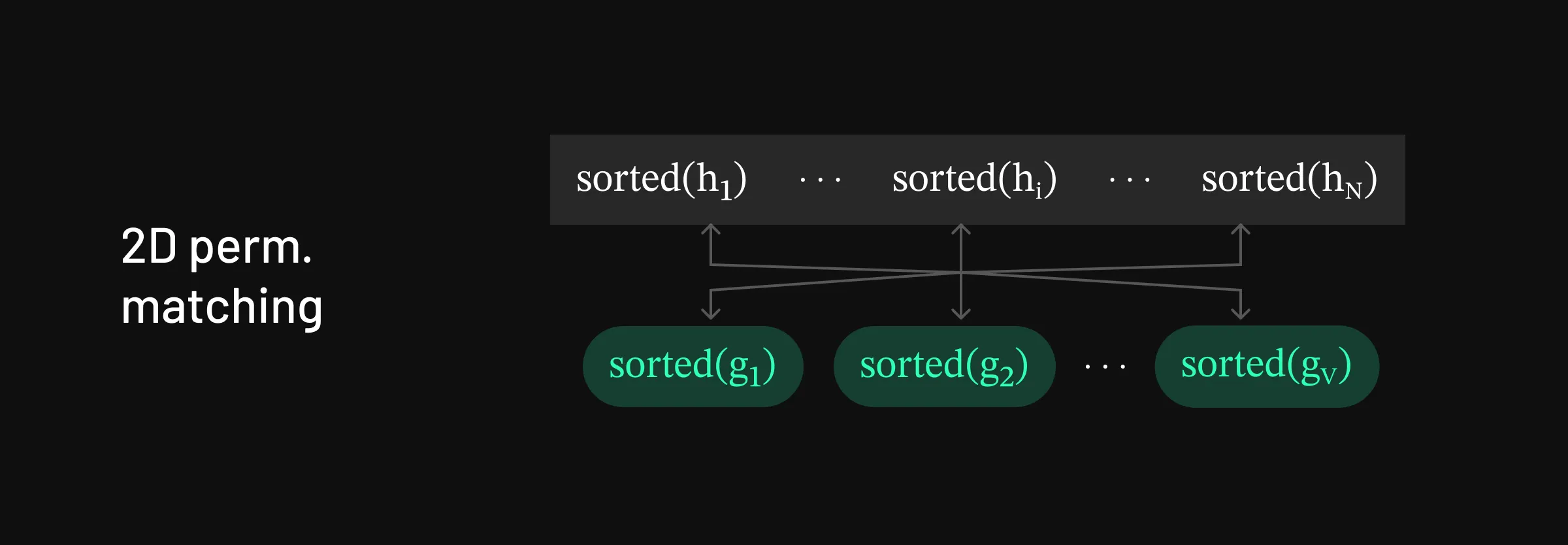 Strategy for matching in the 2D-permuted setting
Strategy for matching in the 2D-permuted setting Finally, we look at ‘factorized’ 2D permutation, which combines the methodologies of both hidden dimension and sequence dimension permutation decoding. Given h=[h1,h2,…,hN], the hidden states are shuffled in the sequence dimension and hidden dimension permutation is applied to each state. This can be written as:
hfact_perm=[π1(hσ(1)),π2(hσ(2)),...,πN(hσ(N))]
where σ is a permutation of [N] and each πi permutes a d-dimensional vector.
The modified attack uses similar ideas as above:
We iterate through tokens in the vocabulary, passing them through the LLM model. We want to find a match for π1(hσ(1)). To address the hidden dimension permutation, we must first sort the candidate and target hidden state to be compared, just as we did in hidden dimension reversal. However, we also don’t know what σ(1) is. So we sort all the hidden states and select the token that matches some hidden state sorted(πi(hσ(i))).
- Again, by the properties of attention, we know there will be exactly one match here.
Now that we’ve found a match for π1(hσ(1)), we discard it and fix the first token. Then we do forward passes over [x1,v] for all tokens v in the vocabulary until we find a hidden state that matches some sorted(πi(hσ(i))).
Repeat this procedure until all of [h1,…,hN] are matched.
And that’s it! Using the above, we are able to decode even this permutation. Importantly, this breaks the plaintext revelation protocol of PermLLM.
Our experiment with 2D permutation shows slightly lower percentages of decoded prompts; however, our metric is a measure of fully decoded prompts. Even in those cases where the prompt was not perfectly decoded, we still observed significant partial decoding.
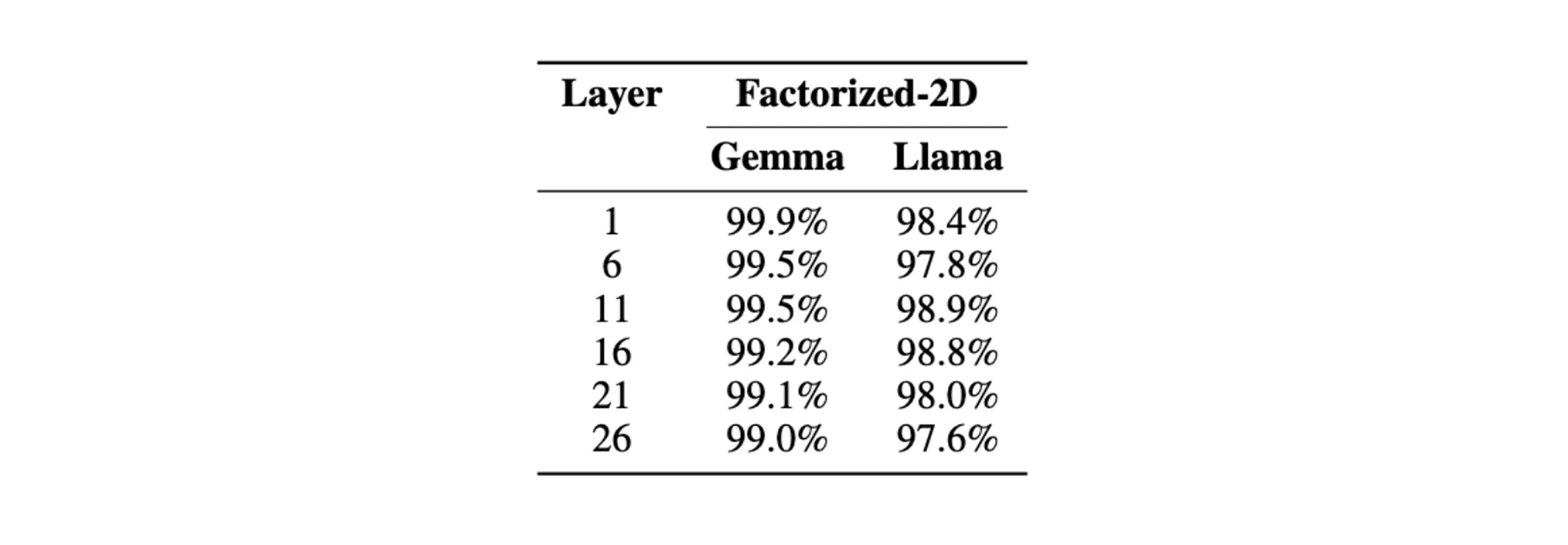
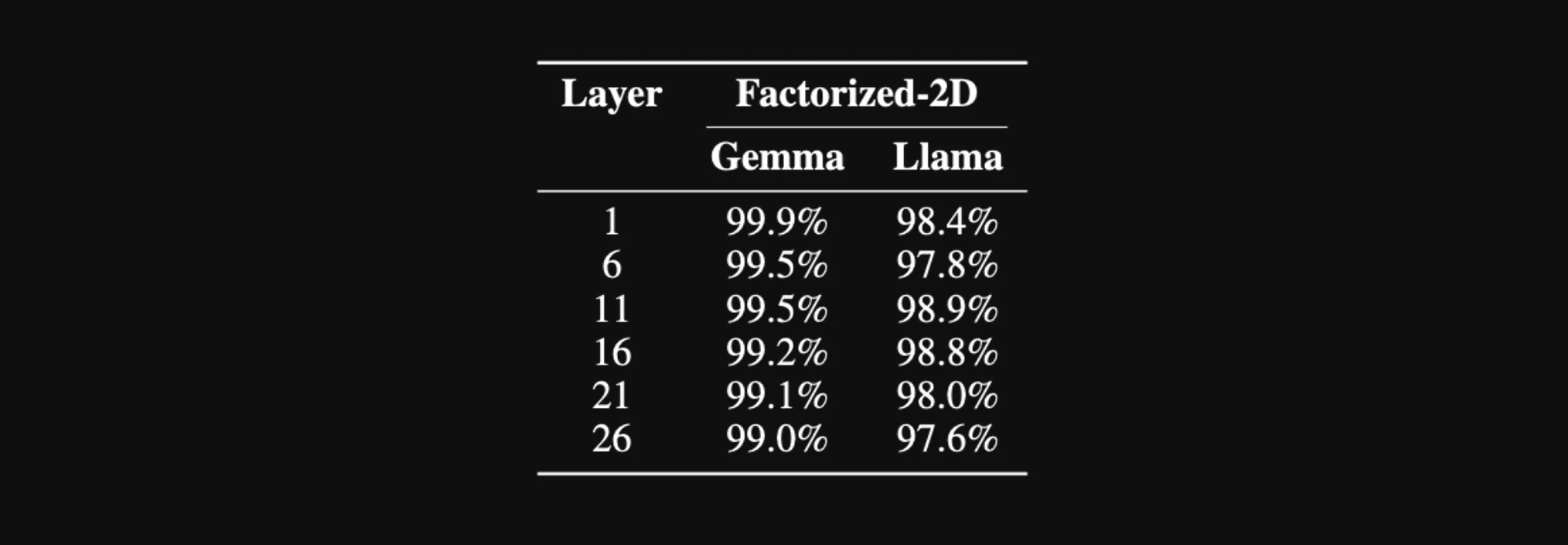 The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the 2D-permuted setting.
The percentage of perfectly decoded evaluation samples by our attack at different layers of Gemma-2-2B-IT and Llama-3.1-8B-Instruct in the 2D-permuted setting. Summary
At the start of this post, we posed a central question for privacy-preserving LLM inference protocols: Is it difficult to recover original prompts from permuted hidden states? Intuitively, the answer seemed like a yes - after all, the permutation space is vast, discrete, and appears computationally intractable to brute-force. However, our results show that by leveraging the structure and behavior of modern decoder-only LLMs, we can drastically cut down the effective search space. In practice, we have devised a fast and effective attack that can reverse-engineer the original inputs, revealing that permutation-based obfuscation is not sufficient for robust security.
Then What Is Secure?
If permutation-based obfuscation fails, where does that leave us? Clearly, any viable solution must do more than shuffle hidden states and hope for the best. To truly secure prompt data during inference, we need mechanisms that fundamentally limit what any single party can observe or reconstruct.
In the next post, we’ll introduce Ritual’s work on a scheme that leverages the above insight.
To cite this blog post, please use:
@misc{breaking-permutations,
title={Breaking Permutation Security in LLM Inference},
author={Arka Pal, Erica Choi, Rahul Thomas, Louai Zahran, Micah Goldblum},
year={2025},
howpublished=\\url{ritual.net/blog/breaking-permutations}
}Disclaimer: This post is for general information purposes only. It does not constitute investment advice or a recommendation, offer or solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. The information in this post should not be construed as a promise or guarantee in connection with the release or development of any future products, services or digital assets. This post reflects the current opinions of the authors and is not made on behalf of Ritual or its affiliates and does not necessarily reflect the opinions of Ritual, its affiliates or individuals associated with Ritual. All information in this post is provided without any representation or warranty of any kind. The opinions reflected herein are subject to change without being updated.